Article rédigé par Charles Miranda et Anthony Nouy (Centrale Nantes, Nantes Université, Laboratoire de Mathématiques Jean Leray UMR CNRS 6629).

L’intelligence artificielle (IA) moderne repose largement sur des modèles de grande taille, entraînés à l’aide de volumes massifs de données et de ressources de calcul considérables. Bien que ces modèles aient permis des avancées spectaculaires, elle soulève aujourd’hui de nombreux défis liés aux coûts énergétiques croissants, à la dépendance à de grandes infrastructures de calcul, et aux difficultés d’interprétabilité et au manque de robustesse des modèles.

Dans ce contexte, un enjeu central est de concevoir de nouveaux modèles frugaux pour l'IA, qui peuvent être appris efficacement avec moins de données et moins de ressources de calcul. Cela implique une meilleure compréhension mathématique des modèles, ainsi que le développement d’algorithmes d'apprentissage dédiés, robustes et certifiés. Les travaux du projet COFNET, co-financé par l'Agence Nationale de la Recherche (ANR), la Deutsche Forschungsgemeinschaft (DFG) et la Région Pays de la Loire s’inscrivent dans cette perspective.

La malédiction de la dimension et les modèles tensoriels

De nombreux problèmes scientifiques consistent à approcher des fonctions dépendant d’un grand nombre de variables (valeurs des pixels d'une image, variables d'espace et de temps dans un modèle physique...). Or, la complexité de ces problèmes croît rapidement avec la dimension d, un phénomène connu sous le nom de malédiction de la dimension.

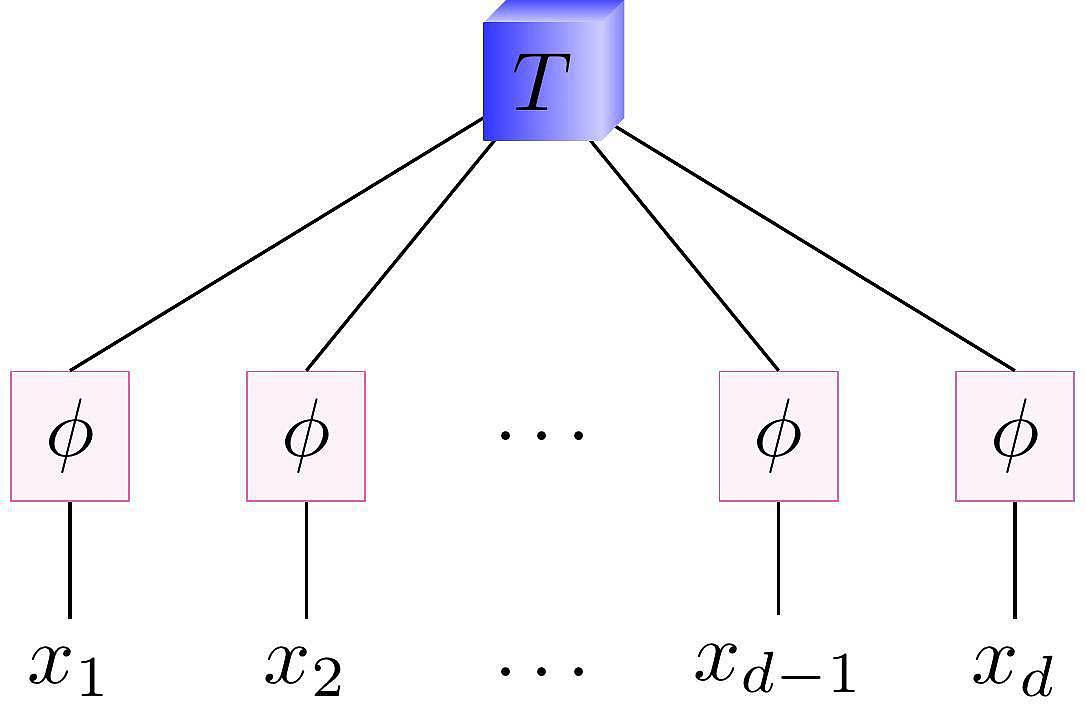
Graphiquement, un modèle tensoriel classique est représenté comme sur la figure 1, où T est un tenseur de coefficients dont le nombre de modes croît exponentiellement avec le nombre de variables d, et les ɸ sont des fonctions données qui extraient de chaque variable x_i un ensemble de caractéristiques ("features").

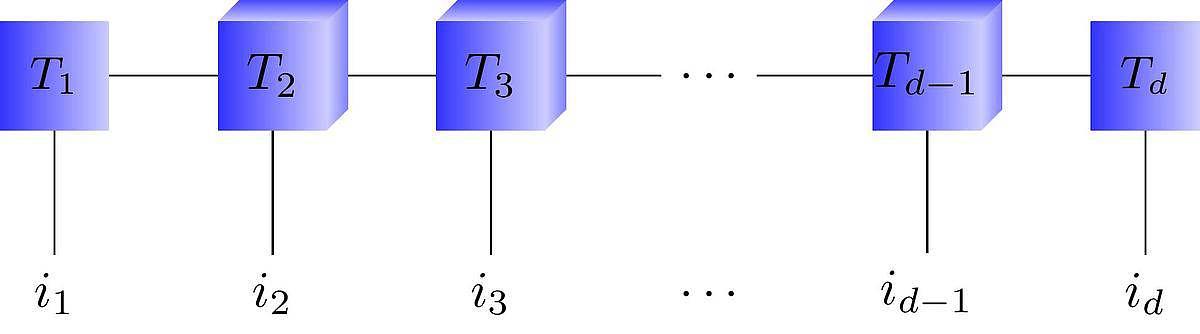
Les formats de tenseurs de faible rang, et en particulier les trains de tenseurs (TT), ont été développés pour y faire face en exploitant des structures particulières des fonctions [1]. Ils consistent à représenter le tenseur T sous la forme "factorisée" représentée sur la figure 2, où les T_k sont de petites matrices ou tenseurs d'ordre 3 dont les dimensions sont les rangs du modèle.

Le modèle résultant a une complexité linéaire en d. Tout d'abord apparus dans le domaine de la physique quantique, ces modèles se sont récemment largement répandus dans le calcul scientifique et l'apprentissage machine. Ces modèles sont très bien maîtrisés d'un point de vue théorique, ce qui a permis le développement d'algorithmes d'apprentissage efficaces. Cependant, leur expressivité (capacité à représenter des données) reste limitée comparée aux architectures modernes de réseaux de neurones.

Vers la composition de tenseurs

Les Compositional Tensor Trains (CTT) proposent une alternative : représenter une fonction complexe comme une composition de transformations simples, chacune étant décrite par des TT de faibles rangs. Plus précisément, une fonction f est approchée sous la forme

f(x) ≈ R o (I + ψ_L) o ... o (I + ψ₁) o L(x)

où L est un opérateur qui extrait de la donnée x des caractéristiques ("features"), les ψ_k sont des fonctions de faible rang, représentées par des TT, et R est un opérateur de projection finale.

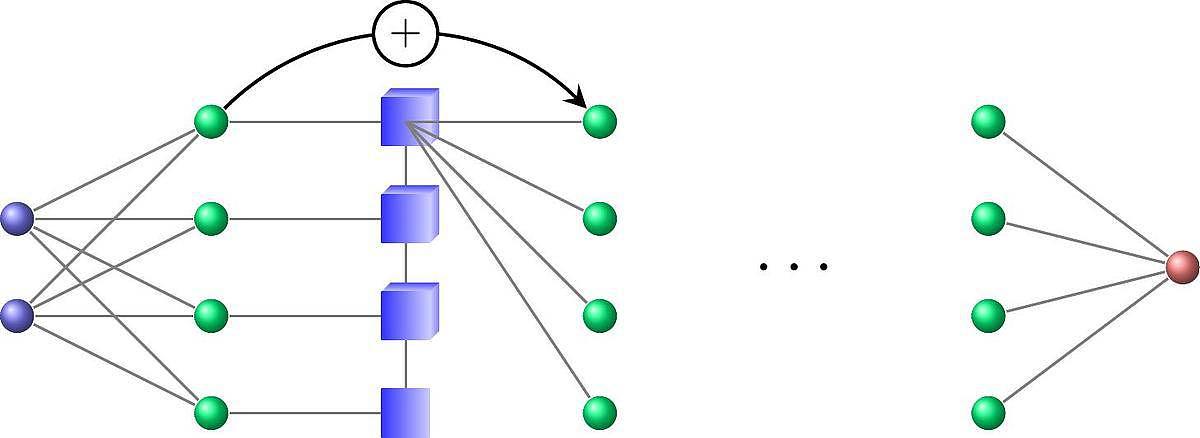
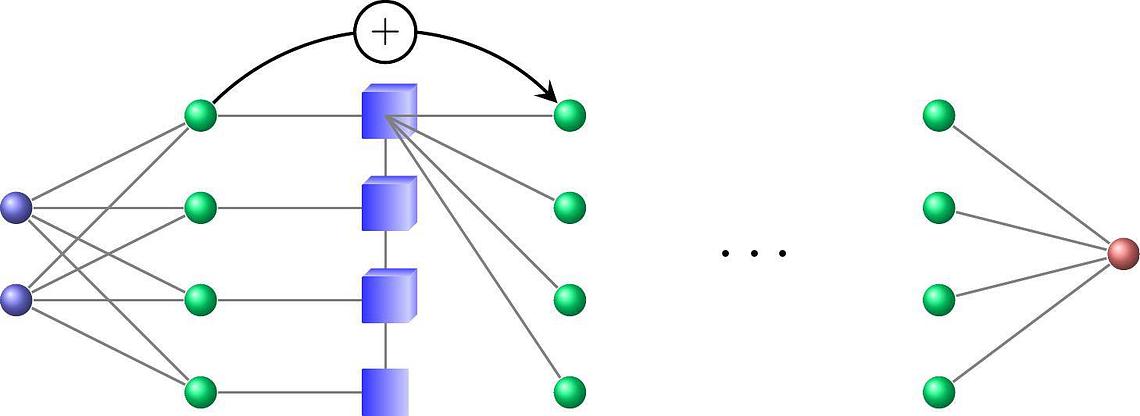
L'architecture résultante, représentée sur la figure 3, est similaire à des architectures de réseaux de neurones profonds à largeur fixe, mais avec une structure mathématique permettant le développement d'algorithmes d'apprentissage et de compression maîtrisés.

Une grande expressivité

Il est démontré dans [2] que les CTT ont au moins le même pouvoir d'expressivité (performance) qu'une large classe de modèles traditionnels incluant les transformations linéaires, les polynômes, et même des réseaux de neurones profonds. Les CTT fournissent donc un outil très puissant, mais reposant sur une architecture bénéficiant de la puissance des outils du calcul tensoriel.

Des algorithmes d'apprentissage plus fiables

Ces travaux proposent également une méthode d’apprentissage dédiée exploitant la géométrie des TT, une algèbre tensorielle efficace, et des outils modernes d'algèbre linéaire aléatoire, qui rendent faisable l'optimisation de tels modèles. Les algorithmes présentent une très bonne stabilité numérique, permettent une réduction des coûts de calcul et, dans certains cas, ils s'accompagnent de garanties théoriques de convergence [3].

Ces méthodes d'apprentissage sont basées sur une méthode de gradient naturel. Contrairement à la descente de gradient standard (avec le gradient euclidien), le gradient naturel tient compte de la géométrie intrinsèque du modèle nonlinéaire. Cette approche permet d'effectuer des mises à jour dans l'espace des paramètres alignées avec la mise à jour dans l'espace des fonctions, et est donc mieux adaptée à la structure du problème, améliorant ainsi la robustesse et la vitesse de convergence.

Ce point de vue fonctionnel permet également de mettre en place des stratégies d'échantillonnage optimal [4], générant des données adaptées pour l'apprentissage de ces modèles, et réduisant ainsi la quantité de données utilisées.

Une piste pour l'IA de demain

Les CTT illustrent une orientation majeure de l’IA contemporaine : développer des modèles structurés et mathématiquement bien maîtrisés. En combinant une grande expressivité et l'existence d'algorithmes d'apprentissage et de compression maîtrisés, ils ouvrent la voie à une IA plus économe en données et en ressources de calcul, mieux adaptée aux enjeux d'application scientifiques et industrielles, et l'utilisation de l'apprentissage machine dans le calcul scientifique.

Bibliographie

1. Oseledets, I. V. (2011). Tensor-Train Decomposition. SIAM Journal on Scientific Computing, 33(5), 2295–2317. https://epubs.siam.org/doi/10.1137/090752286
2. Eigel, M., Miranda, C., Nouy, A., & Sommer, D. (2025). Approximation and learning with compositional tensor trains. https://arxiv.org/abs/2512.18059
3. Gruhlke, R., Nouy, A., & Trunschke, P. (2024). Optimal sampling for stochastic and natural gradient descent. https://arxiv.org/abs/2402.03113v2
4. Nouy, A., & Michel, B. (2025). Weighted least-squares approximation with determinantal point processes and generalized volume sampling. SMAI Journal of Computational Mathematics, 11, 1–36. https://smai-jcm.centre-mersenne.org/articles/10.5802/smai-jcm.117/